PARABOLAS Y HIPERBOLAS

CONCEPTO DE PARABOLA
ES EL CONJUNTO DE PUNTOS EN EL PLANO QUE SE MUEVEN A TAL MANERA QUE SIEMPRE EQUIDISTAN DE UN PUNTO FIJO Y UNA RECTA FIJA, A LAS CUALES SE LLAMA FOCO O DISECTRIZ.
ELEMENTOS DE UNA PARABOLA
NOS AYUDARA A FORMAR CORRECTAMENTE LA PARABOLA DENTRO DE UNA PLANO CARTESIANO, SI ALGUNO DE ESTOS ELEMENTOS NO COINCIDEN COMO DEBEN SER ENTONCES NOS DAREMOS CUENTA QUE HICIMOS ALGO INCORECTO.
 ELEMENTOS DE LA PARABOLA:
  


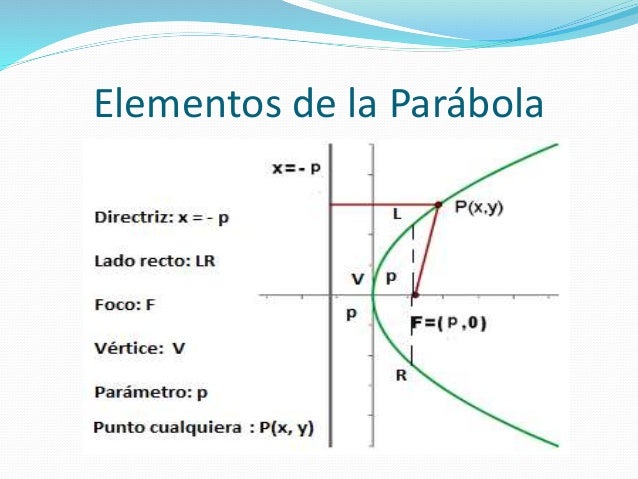
Una parábola es una curva en la que los puntos están a la misma distancia de:

• un punto fijo (el foco), y
• una línea fija (la directriz)

HIPERBOLAS
CONCEPTO:
ES EL LUGAR GEOMETRICO DE UN PUNTO QUE SE MUEVE EN UN PLANO DE TAL MANERA QUE EL VALOR ABSOLUTO DE LAS DIFERENCIAS A DOS PUNTOS FIJOS DEL PLANO, LLAMADOS FOCOS, ES SIEMPRE IGUAL A UNA CANTIDAD CONSTANTE, POSITIVA Y MENOR QUE LA DISTANCIA ENTRE LOS FOCOS.
ELEMENTOS DE UNA HIPERBOLA 


 

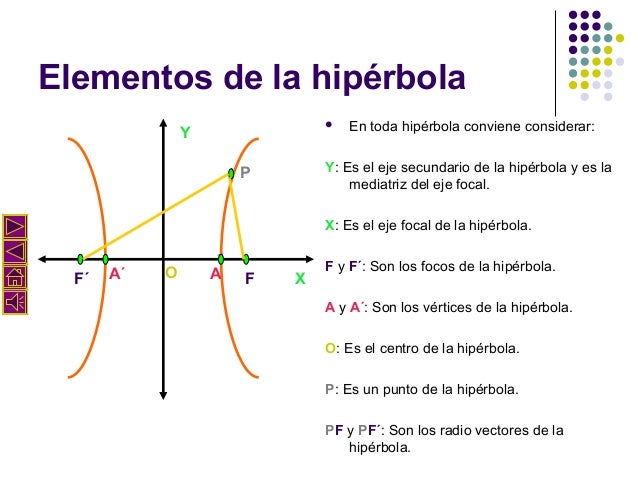
Eje mayor o real

El eje mayor es la recta de la hipérbola donde pertenecen los focos y los vértices de la misma. Su valor es 2a y es perpendicular al eje imaginario

Eje menor o imaginario.

El eje menor o imaginario no tiene puntos en común con la hipérbola. Sin embargo, siempre se cumple que las perpendiculares lanzadas por sus extremos cortan con las perpendiculares lanzadas por los extremos del eje mayor en 4 puntos que pueden servir para trazar las asíntotas.

Asíntotas

Son las rectas r y r' que pasan por el centro de la hipérbola y verifican que se acercan ramas de la misma tanto más cuanto más nos alejamos del centro de la hipérbola.
Las ecuaciones de las asíntotas son: r: y= b/a x r': y = -b/a x

Vértices

Los vértices de una hipérbola son los puntos donde ésta corta a sus ejes.

Focos

Son dos puntos, , respecto de los cuales permanece constante la diferencia de distancias (en valor absoluto) a cualquier punto, , de dicha hipérbola.

Centro

Punto medio de los vértices y de los focos de la hipérbola.

Tangentes

La tangente a una hipérbola en cualquier punto de la curva es bisectriz del ángulo formado por los radios vectores de ese punto

OBJETIVOS
 La enseñanza de las Matemáticas tendrá como objetivo contribuir a desarrollar, en los alumnos y alumnas, las  capacidades de  Identificar, analizar y resolver situaciones y problemas de su medio

EJERCICIOS

DESCARGAR



referencia:
https://es.scribd.com/doc/1409750/TEORIA-DE-HIPERBOLAS
https://es.slideshare.net/18Primavera62/teoria-de-la-parbola
https://es.slideshare.net/meche_rc10/la-parbolapps
https://www.matematicaparatodos.com/ANALITICA/7_EJERCICIOS_HIPERBOLA.pdf